密码学

简单来说，密码学是一种用来研究如何加密来保护信息，如何解密获取信息的学问。

为什么学密码

可以了解、开创并实现现代密码学的 RSA 算法、未来将抵御量子计算机的格密码等的「后量子密码技术」，以及学到在特殊情况下我们用现代计算机来破解特定的 RSA 现代密码和后量子密码技术的攻击手段。

密码有清晰的路线学习：

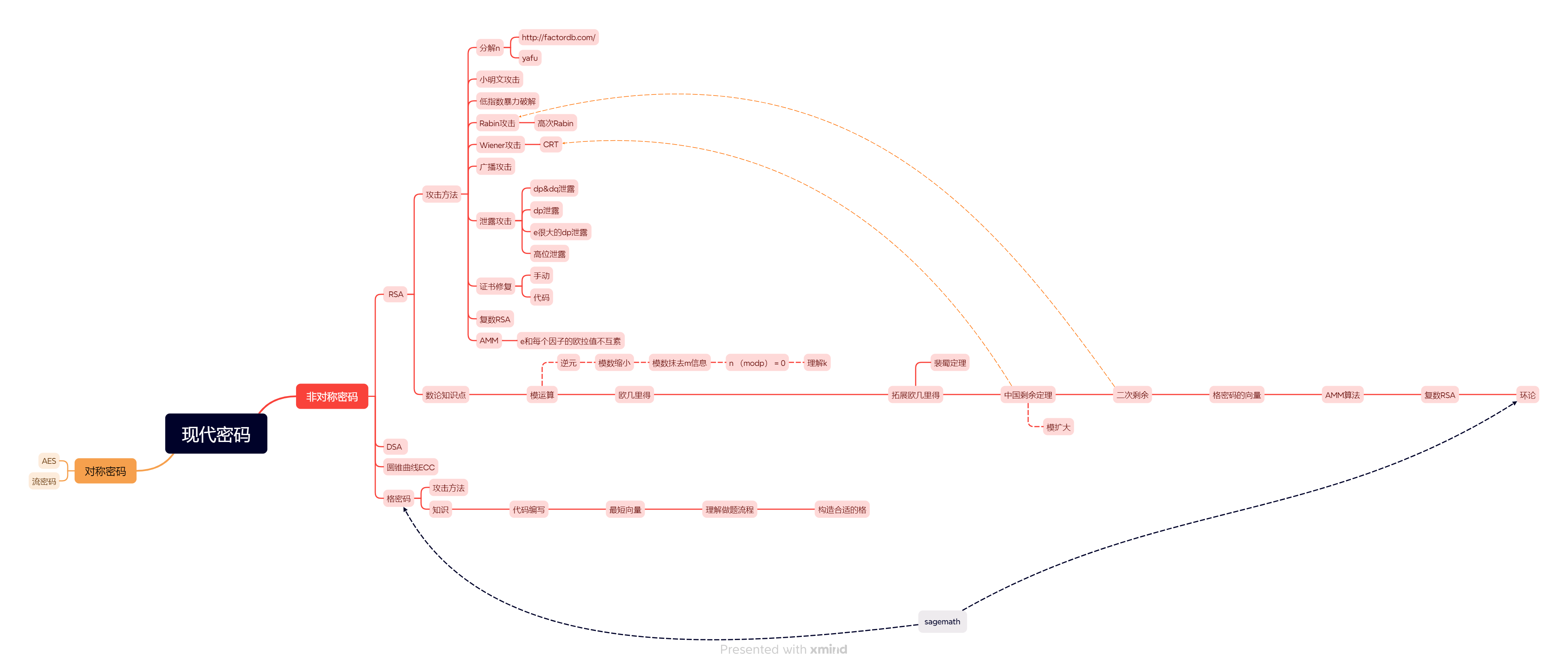
并且有干脆的做题反馈，就跟数学题一样，会就是会，不会就是不会。

或者说没有理由，当你入门密码学的时候，就会发现做密码题也会上瘾！

准备工作

你需要准备以下工具：

• PC（一般不限操作系统）
• Python 编程语言和环境
• yafu 软件程序
• 一款笔记软件或网站
• 草稿纸和笔（随电脑携带的，经常需要演算关系式）
• 大数分解 factordb 网站

其它一些帮助性较大的网站：

• NSSCTF 探索商城
• CTF Wiki
• OI Wiki（包含一些更深的数学知识）

除此之外，在学习的途中还会遇到很多有意思的工具或网站。

学习路线

Python 编程基础

下载 Python，选择一款集成开发环境（IDE，如 PyCharm 或 VSCode），并配置好 Python 环境。

由于国内使用 Python 的包管理工具下载缓慢，可参照 清华大学软件源 PyPI 配置镜像源。

使用 Python 的包管理工具安装必要的密码学库：

pip install pycryptodome
pip install gmpy2

在 Python 的学习中，你必须了解：

• 变量和变量类型，变量类型转换
• 运算符号
• 基本语法
• 循环语句
• 布尔类型
• 列表和元组
• 模块导入
• 函数的使用
• Python 中各种进制的格式头

你可以通过解释如下代码片段中高亮行的含义来检验自己的学习情况（下面的代码整体无实际意义）：

from Crypto.Util.number import *
import gmpy2

flag = b"flag{test_flag}"
flag = bytes_to_long(flag) 

e = b'65537'
e = int(a) 

plist = [2, 3, 5, 7, 11, 13, 17, 19, 23, 29] 
plist = tuple(plist) 

p = getPrime(256)
q = 0xda1a92b4bf451ce51f14a1d178e224a237f3e7e4b18a60084ae7da91889830b1
n = p*q

c = pow(flag, e, n) 

x = c % p // 2

密码学基础

你需要了解下面这些知识点：

• 理解模运算
• 逆元计算的运用（暂时不要求理解）
• RSA 公钥加密算法（可参考文章：RSA 入门）
• 理解海纳百川的 $k$ 和无所不能的公因数

开始学习

（一）掌握一定语言基础

首先建议学 Python，密码题经常出现很大的数字和较难的运算，靠手算很难得到答案，所以需要一门计算机语言来帮我们计算。而 Python 是较符合人类直觉并且易用的语言，可以快速编写实现一个功能，对于新手而言最为友好，故推荐从 Python 入门编程语言。

对于学习 Python，了解以下知识点即可（摘自 Python 基础教程 | 菜鸟教程）。

• Python 基础教程
• Python 简介
• Python 环境搭建
• Python 中文编码
• Python 基础语法
• Python 变量类型
• Python 运算符
• Python 条件语句
• Python 循环语句
• Python While 循环语句
• Python for 循环语句
• Python 循环嵌套
• Python break 语句
• Python continue 语句
• Python pass 语句
• Python Number（数组）
• Python 字符串
• Python List（列表）
• Python 日期和时间
• Python 函数
• Python 模块

撰稿人注

讲讲我个人学习 Python 的经历：我一开始就买了本 Python 的入门书籍开始「啃」，啃到后面 for 循环就开始做题了。一开始也不会做题，就看别人的 WriteUp（看看别人的思路，抄作业，但这是个好的行为，大伙开始都是看过来的），WriteUp 里一般都会有 Python 代码，就跟着打在自己的电脑上（建议不要直接复制粘贴），遇到不会的就上网搜索，一边学密码学，一边练编程技术。

编者注

编者具有其它程序语言的基础，对 Python 也只随便看了一些基本的语法（运算、循环）之后便上手密码学了。刚开始做题很艰难，几乎写每一行功能性代码都要网上去搜索（诸如用什么库、函数），经历过大约半个月的持续边做题边编程、看 WriteUp、赛后与前辈交流，Python 能力也见长了。遇到不会的立即学习并应用，慢慢地也就无师自通了。

（二）了解 RSA 算法（公钥加密算法）

「毫不夸张地说，只要有计算机网络的地方，就有 RSA 算法。」

——阮一峰

1. 元素

RSA 算法里面一共有 8 个元素。

• $p$，一个素数。
• $q$，另一个素数
• $n$，根据 $p$ 和 $q$ 形成的数，一般为 $n=p\times q$
• $e$，一个被称为「公钥因子」的数
• $d$，一个被称为「私钥因子」的数。下面的公式会具体展现e和d的转化
• $\phi$，一个与 $n$ 有关，由 $p$ 和 $q$ 计算而得到的数。具体就是 $n$ 的欧拉函数 $\phi (n)$
• $m$，明文，就是要保护的信息。
• $c$，密文，就是要破解的信息。

下面的公式会具体展现明文和密文的转化。

2. 公式

RSA算法中有以下公式

1. 加密公式

$$c\equiv m^e(\mathrm{mod}n)$$

2. 解密公式

$$m\equiv c^d(\mathrm{mod}n)$$

3. $e$ 和 $d$ 的关系式

$$d\equiv e^{-1}(\mathrm{mod}\phi )$$

4. $p$ 和 $q$ 是素数的情况下，$n$ 的欧拉函数

$$\phi =(p-1)(q-1)$$

5. $n$ 与 $p,q$ 的关系式

$$n=p\times q$$

1. 大小关系

$$\begin{array}{c}m<n\\ n\approx \phi \end{array}$$

入门后可以尝试推导一下上面的公式，入门前只需懂得如何在 Python 中实现上面公式即可。

3. 原理

• 解密原理

  一般 RSA 算法加密会公开公钥 $n$ 和 $e$，信息传输难免会泄露密文 $c$，所以我们可以得到的一共有三个元素 $n,e,c$. 从上面的解密公式可以知道我们需要密钥因子 $d$，而计算 $d$ 需要 $e$ 和 $\phi$，$e$ 已知，求未知的 $\phi$ 又需要 $p$ 和 $q$，有关 $p$ 和 $q$ 的式子只有一个 $n=p\times q$.

  因此解密的关键是在得到 $p$ 和 $q$.

  

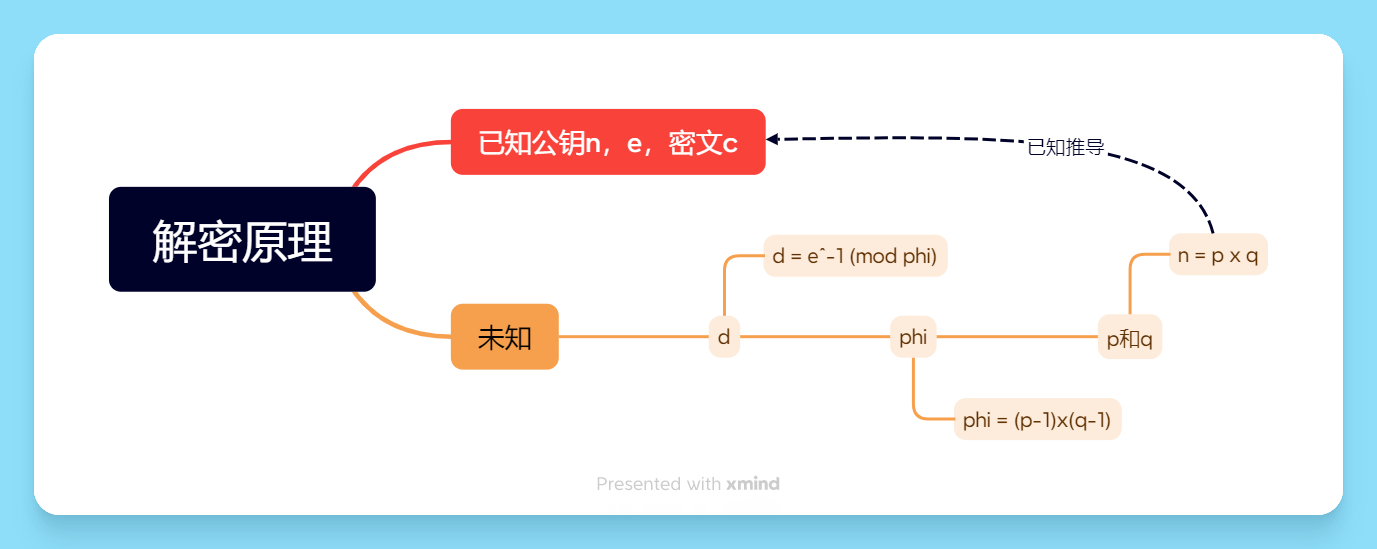
• 难破解的原理

  RSA 算法开创了现代密码并实现了非对称加密，其中难破解的原理基于大整数分解。

  计算 $n=p\times q$ 简单，但由 $n$ 分解出 $p,q$ 非常困难，这是 RSA 算法的基础。

  对于较小的整数，手算数 $12$ 的因子，很快可以列出 $1,2,3,4,6,12$，但一旦上升到很大的整数，例如 6969872410035233098344189258766624225446081814953480897731644163180991292913719910322241873463164232700368119465476508174863062276659958418657253738005689，就极难拆成两个数字。

• 解题的原理

  上面说到，$n$ 很难分解，那我们是靠什么来破解的呢？

  答：靠一个个特殊的情况，有时候出题人会给出泄露的 $d$，或者 $p$ 和 $q$ 之间的关系让我们数学推导等等特殊情况。针对这一个个特殊情况，我们也有相应的攻击方法，例如：

  • 小明文攻击
  • 低指数暴力破解
  • Rabin 攻击与中国剩余定理的初始应用
  • 小明文攻击
  • 广播攻击
    • 低加密指数
    • 不互素的 CRT
  • 拓展欧拉定理
  • Rabin 进阶
  • dp & dq 泄露
  • $p-1$ 光滑
  • AMM
  • RSA 证书
    • 手动处理
    • 代码处理
  • 变种 RSA — SchmidtSamoa
  • 复数与 RSA

4. 数学基础

RSA 中涉及到我们之前没有或者说不太重视的一些数学知识点，接下来我们一起来学习一下。

• 取模

  之前提到的公式中四个有三个都出现了一个英文单词 mod，在数学中，这被称为「模」，是一种运算，即求余运算，编程语言中常以 % 展现。例如，$17÷5=3\cdots 2$，则 17 % 5 = 2，或者记作 $17\equiv 2(\mathrm{mod}5)$. 很容易发现，$17(\mathrm{mod}5)$ 的值域只有 $[0,5)$ 中的整数。

• 模运算

  模运算和平时的运算基本上没有太大区别，只是在模运算中，我们人为的划定了一个整数集合 $[0,n)$，模运算结果都不会超过这个集合。模运算也可以实现等式左右两边交换，例如 $e$ 和 $d$ 的关系式也可以写成 $e\times d\equiv 1(\mathrm{mod}n)$.

  而运算符号加减乘除的除就有些变化了。上面的 $e^{-1}$ 可以写成 $\frac{1}{e}$，但在模运算中不能直接除，

  例如 $\frac{a+1}{b-1}(\mathrm{mod}n)$ 要先求b的逆元 $(b-1{)}^{-1}$，再将这逆元 $(b-1{)}^{-1}$ 与 $(a+1)$ 相乘。

  在上面第三个公式 $e$ 和 $d$ 的关系式中有 $d^{-1}$，这涉及到模运算中求逆元，这点展开会涉及到其他数学知识，这里先放着不谈。只要记住在模运算中，没有除法，只有求逆元然后再相乘。具体的代码实现会在下面讲述。

• 海纳百川的 $\mathit{k}$ 和无所不能的公因数

  在上面的取模和模运算中，涉及到大量的 $\mathrm{mod}n$ 操作，如何转化成可以手算推理的东西呢？

  答：$k\times n$，其中 $k$ 是任意整数，例如 $12(\mathrm{mod}5)=12-2\times 5$，其中 $k=2$.

  我们之后会遇到一部分的数学推导题，题目会给出有关 $p$ 和 $q$ 的关系式。草稿纸上推理处理完关系式后，经常能得到一个有关 $p$ 或者 $q$ 的式子 $a\equiv b(\mathrm{mod}p)$，此时我们只需要将这个式子转化一下

  $$a=b+k_{1}p\Rightarrow k_{1}p=a-b$$

  然后求 $a-b$ 和 $n$ 的公因数就可以得到 $p$ 了。

  因为 $n=p\times q$ 也可以看成 $n=k_{2}p$，而一般 $k_1\ne k_2$，所以就可以得到 $p$.

  INFO

  具体情况可参见 羊城杯 2021 Bigrsa 共享素数。

5. 计算机基础

思考这样一个问题：将字符串 我喜欢密码学 转化为整数。

这看起来有点不可思议，文字和数字怎么联系在一起。但计算机上就可以，计算机底层是一堆二进制，只有 0 和 1。要想在屏幕上展现文字，就需要编码。编码将数字按照一定的法则转换成对应的文字，常见的编码如 ASCII 编码。

通过一些编码方式，我们就能把想保护传输的信息转换成整数并一一对应，再通过 RSA 算法加密计算得到密文 $c$.

$$c\equiv m^e(\mathrm{mod}n)$$

6. 代码实现

加密脚本不需要掌握熟背，只需知道每一行的意思即可；解密脚本需熟练掌握。

RSA 加密脚本

# 导入 Crypto.Util.number 模块中的所有函数
from Crypto.Util.number import *
# 导入 gmpy2 模块，用于高性能的数学运算
import gmpy2
# 从 secret 模块导入 flag，通常用于表示隐藏信息
from secret import flag

# 这是给出了 flag 的样式，并不是真正的 flag，但已经提供了一些提示，有些题目会根据 flag 头来破解
flag = b"NSCTF{******}"

# 生成两个 256 位的质数 p 和 q
p = getPrime(256)
q = getPrime(256)

# 计算 n，即 p 和 q 的乘积，用于 RSA 算法的模数
n = p * q
# 定义公钥指数 e，通常为 65537
e = 65537
# 将 flag 转换为长整数
m = bytes_to_long(flag)

# 使用 gmpy2 模块的 powmod 函数进行模幂运算，加密消息得到密文 c
c = gmpy2.powmod(m, e, n)

# 打印模数 n
print(f'n = {n}')
# 打印公钥指数 e
print(f'e = {e}')
# 打印加密后的密文 c
print(f'c = {c}')
# 打印质数 p（通常在 CTF 中不会直接给出）
print(f'p = {p}')
# 打印质数 q（通常在 CTF 中不会直接给出）
print(f'q = {q}')

# 以下是输出的结果，这些值通常在 CTF 题目中给出
# n = 4024941574680124502316363981547051098032677531528457166859670261861728313081282635664023890534034586556845494323497683923813915739234466472396261320600483
# e = 65537
# c = 226967182640114431119923862488626190608050511354278604627242247124377735518111678279381846350389469161980779137969837090666693533616114290831130137310320
# p = 62658315832909660478685872111870233686035497063073558738980225214351386198939
# q = 64236351092062515945998729497153532140067861836088195242257976217499252460697

RSA 解密脚本

# 导入 Crypto.Util.number 模块中的所有函数，用于处理数字和字节之间的转换等
from Crypto.Util.number import *


"""输入部分"""
# 已知的模数 n，用于 RSA 加密和解密
n = 4024941574680124502316363981547051098032677531528457166859670261861728313081282635664023890534034586556845494323497683923813915739234466472396261320600483
# 已知的公钥指数 e，通常为 65537
e = 65537
# 已知的密文 c，需要被解密
c = 226967182640114431119923862488626190608050511354278604627242247124377735518111678279381846350389469161980779137969837090666693533616114290831130137310320
# 已知的质数 p，用于计算私钥
p = 62658315832909660478685872111870233686035497063073558738980225214351386198939
# 已知的质数 q，用于计算私钥
q = 64236351092062515945998729497153532140067861836088195242257976217499252460697


"""处理部分"""
# 计算欧拉函数 phi(n)，用于RSA算法中的私钥计算
phi = (p-1)*(q-1)
# 计算私钥指数 d，即 e 在模 phi(n) 的逆元
d = inverse(e,phi)
# 使用私钥指数 d 解密密文 c，得到明文 m，具体就是 m = c ** d (modn)
m = pow(c, d, n)
# 将解密后的长整数 m 转换回字符串，得到原始的 flag 信息
flag = long_to_bytes(m)


"""输出部分"""
# 打印解密后的 flag 信息
print(flag)

以后的路

入门 RSA 算法后，可以选择跟着 NSSCTF 的工坊课程 自主继续深造 RSA，在这基础上一起学习 AES 对称加密、圆锥曲线算法、LCG 流密码、格密码和 DSA 密码等等。

写在最后

密码路上道阻且长，希望同学们能坚持下去，必定能见到密码学的彩虹！